One of the first things most people do in the morning is turn on a tap in the bathroom. Provided we are not too sleepy, we cannot fail to notice what is often considered to be the greatest unsolved mystery in classical physics: turbulence. If we turn the tap just a little, the flow of water is smooth and laminar. However, as we open it more, the flow becomes irregular and turbulent.
As physicists, we would like to have a theory that explains this phenomenon. But a complete understanding of turbulence in ordinary classical fluids remains elusive. Now Frans Nieuwstadt of the Delft University of Technology in the Netherlands and co-workers have performed an experiment that could take us closer to this goal. By studying the flow of water in a long pipe, the team has observed travelling-wave patterns during the transition from smooth to turbulent flow for the first time. Moreover, the results are in good agreement with recent predictions (B Hof et al. 2004 Science 305 1594).
Reynolds’ puzzle
The problem of turbulence goes back to 1883, when Osborne Reynolds of Manchester University made a remarkable discovery that has remained a puzzle ever since. By injecting a small amount of ink into a horizontal glass pipe filled with water, he was able to check whether the flow was laminar or turbulent. Reynolds found that the transition from laminar to turbulent flow occurs spontaneously if a dimensionless quantity, R, is larger than 2000.
This quantity, which is known as the Reynolds number, is defined as the ratio of the inertial and viscous forces on the fluid: R = VD/v, where V is the mean velocity of the flow, D is the diameter of the pipe and v is the viscosity of the fluid. We now know that Reynolds’ initial figure of 2000 varies from experiment to experiment. Indeed, by carefully controlling the flow at the inlet of the pipe, laminar flows can be sustained at Reynolds numbers up to 100,000.
From direct observations of fluids like those carried out by Reynolds, researchers know that the profile of a fluid during laminar flow is parabolic. This is also clearly seen by solving the Navier-Stokes equation, which forms the basis of classical fluid dynamics. So why does the flow suddenly become unstable and break up into turbulent swirls at large enough values of R?
The standard way to answer this kind of question is to study the response of a fluid when it is subject to infinitesimally small disturbances, using a mathematical tool called linear stability theory. For example, imagine carefully placing a ball at the top of a perfectly smooth hill. If we gently nudge the ball, it will roll down away from the top. On the other hand, if we place the ball in a valley between hills and then perturb it, it will come back to its rest position. We therefore conclude that the bottom position is stable, while the top position is unstable.
Infinitesimal instabilities
When applied to the infinite degrees of freedom in a fluid, linear stability theory predicts a great variety of phenomena – from thermal convection to vortex formation in rotating flows. Typically, one begins with a simple “primary” solution of the Navier-Stokes equation and then tracks this solution while increasing some parameter that drives the disturbances. At some critical value of the drive parameter, the primary solution becomes unstable and a new solution branches out with a more complex flow pattern, a process called bifurcation.
In the case of a fluid in a pipe, the primary solution is the parabolic profile and the drive parameter is R. Unfortunately, the theory fails miserably in predicting any bifurcation: the parabolic profile is always stable, even if R becomes infinite! This direct contradiction of Reynolds’ experiment is surprising, since the tiny disturbances in linear stability theory represent the mechanical vibrations and thermal noise that are unavoidable in any physical system. Indeed, even computer simulations are subject to such disturbances as a result of rounding and truncation errors. So what is so special about a fluid in a pipe?
Since infinitesimal perturbations do not appear to trigger turbulence, the culprit must be perturbations with a larger amplitude. Indeed, Tom Mullin of Manchester University and co-workers, including Björn Hof, who was also involved in the Delft experiment, recently repeated Reynolds’ experiment with extraordinary care, and found that the amplitude of the perturbations required to establish turbulence scales inversely with R (B Hof et al. 2003 Phys. Rev. Lett. 91 244502).
Mathematically, such finite amplitudes are bad news because they mean that one has to face the full nonlinearity of the Navier-Stokes equation. But some applied mathematicians have risen to this challenge. Richard Kerswell of Bristol University in the UK, Fabian Waleffe of the University of Wisconsin and Bruno Eckhardt of Philipps University in Marburg, Germany – who also participated in the Delft experiment – have discovered a new class of travelling-wave solutions to the Navier-Stokes equation that exist for values of R above approximately 1200. These solutions are unstable since they are not related to the primary branch of the parabolic profile, and obtaining them required a mathematical tour de force.
Kerswell and co-workers mapped the pipe scenario onto a more general problem with an additional drive parameter, for which a bifurcation can be found. The new solution branch was then tracked back to the point where the second drive parameter vanishes, leaving a new solution to the original pipe-flow problem that is disconnected from the primary parabolic profile. The new, unstable travelling-wave solutions consist of flow-wise swirls and streaks with rotational symmetry about the axis of the pipe. It now seems that these solutions have been observed in an experiment.
Experimental solution
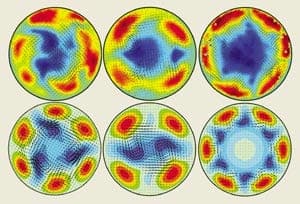
To investigate the transition from laminar to turbulent flow, Nieuwstadt and co-workers injected water into a pipe 26 m in length. They then studied the region of turbulent flow that was produced further down the pipe using a particle image velocimeter (a combination of high-speed cameras and pulsed lasers) to measure the whole velocity field across the flow at very high repetition rates. Impressively, the Delft team observed transient flow structures with 2-, 3-, 4- and 6-fold symmetry that are very similar to the new travelling-wave solutions (see figure).This transition to turbulence can be likened to pinball. The flow undergoes erratic behaviour whereby it moves from one unstable solution to another before returning to the primary parabolic profile. This happens because more travelling waves appear as R is increased, which can attract trajectories from most other directions in phase space. The unstable waves form an attracting region of trajectories that becomes larger and larger, whereas the basin of attraction of the parabolic profile shrinks. In other words, perturbations of smaller amplitude become large enough to trigger turbulence in agreement with Mullin’s finding.
This breakthrough is the result of a remarkable collaboration between applied mathematicians and physicists. The feeling of wonder inspired by watching a turbulent flow can only be matched by the breadth of application and predictive power of the Navier-Stokes equation. Although this short, innocent-looking equation was devised 150 years ago, it seems we still have to unlock all of its secrets.
